Fun with Globes: How to Make a Cubical Earth


Recently, one of our users asked about projecting the earth onto a gnomonic cube. While it isn’t often you’d want to look at the world this way, the result is visually interesting, and it wasn’t immediately obvious how to do it. I’d like to share my experience and some of the resulting images here. (Interested in geographic puzzles? Dan Koopman recently posted a great story on the University of Vermont’s SAL blog.)
Gnomonic what?
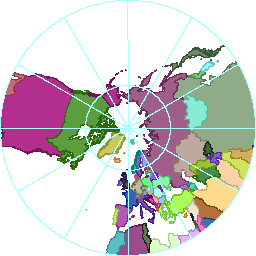 The gnomonic projection is a way of flattening the earth while preserving the property that the shortest path between any two points is a straight line. Straight lines on the flattened map correspond to great circle arcs on the globe, and vice versa. One consequence is that you can’t map much of the earth without large distortion (30°N+ shown here), with the hard limit just shy of a full hemisphere. There are other projections that can be used to form a cube (e.g., a conformal one, and one Esri uses for ArcGlobe), so gnomonic isn’t unique in this regard.
The gnomonic projection is a way of flattening the earth while preserving the property that the shortest path between any two points is a straight line. Straight lines on the flattened map correspond to great circle arcs on the globe, and vice versa. One consequence is that you can’t map much of the earth without large distortion (30°N+ shown here), with the hard limit just shy of a full hemisphere. There are other projections that can be used to form a cube (e.g., a conformal one, and one Esri uses for ArcGlobe), so gnomonic isn’t unique in this regard.
A False Start
My first stop was Carlos Furuti’s fantastic site, which has a wealth of pictures and information about polyhedral maps in general (the gnomonic cube being just one example). I get the sense that if I looked hard enough, I’d have found all the instructions there, but it didn’t work out. John Savard’s site assured me that the projection can be “employed fairly simply” to make the cube. Knowing that the map had to line up at the edges, and that these edges — as straight lines — would correspond to great circle arcs, I looked for places to cut the globe. My first attempt was to divide the earth into six parts along the equator and 120°W, 0°E, and 120°E meridians, with gnomonic projections centered on each part. This yielded six rectangular triangles, which couldn’t be formed into a cube.
The Secret
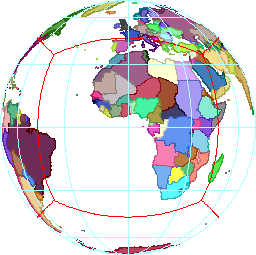 One way that does work is to center one face of the cube on each pole, with the remaining faces in between. I figured out the polar cut lines by including 45° of travel from the pole in each of the four natural directions (along the 90°W, 0°E, 90°E, and 180°E meridians), and then filling in the rest of the square. The meridian cut lines are spaced 90° apart, and are offset so the equatorial faces are centered on the meridians listed above. In total, the cut lines (shown here) result in six square faces that line up along great circle arcs, just as we needed.
One way that does work is to center one face of the cube on each pole, with the remaining faces in between. I figured out the polar cut lines by including 45° of travel from the pole in each of the four natural directions (along the 90°W, 0°E, 90°E, and 180°E meridians), and then filling in the rest of the square. The meridian cut lines are spaced 90° apart, and are offset so the equatorial faces are centered on the meridians listed above. In total, the cut lines (shown here) result in six square faces that line up along great circle arcs, just as we needed.
Conclusion
With the six projected faces in hand, it’s straightforward to assemble them into a cube (shown here). Why might you care?
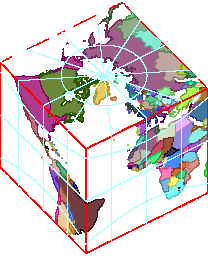
- It looks cool.
- You can still use the “pull a string tight between two locations to find the shortest path” trick, as long as you make sure the string goes over the right edges.
- These kind of projections can be used to texture spheres in 3D applications; e.g. see this research paper from Microsoft, especially the great pictures on Page 20.
- Finally, you can use your reaction to the gnomonic cube (hate it? love it?) and other projections to learn something about yourself.
How are you using map projections to visualize our world?



